I recently was exploring the Golden Ratio. I was really surprised what a simple (and recursive) relationship it comes from:
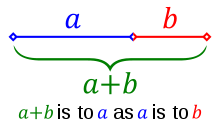
Starting with this this image, here is the derivation of the golden ratio...
From this relationship we see in this image, we can derive this equation: \[\frac{a}{b} = \frac{a+b}{a}\]
And if we then let b=1 (so we can find the ratio of a to 1), we get: \[a = \frac{a+1}{a}\]
Then, with this formula, we can define a function: \[f(a) = \frac{a+1}{a}\]
If we then find the fixed-point in this function (so that f(x) = x), then we will have found a solution to \[a = \frac{a+1}{a}\]
A simple way to think about the fixed-point of this function is this: it is the place where \(y=x\) (or \(f(x) = x\) ) intersects with our function. And that intersction point should be the golden ratio.
# Plot y=(x+1)/x and y=x
x=numpy.linspace(0.5,3,1000)
y=map(lambda a: (a+1.0)/a, x)
y2=map(lambda a: a, x)
plot(x, y)
plot(x, y2, 'r')
# Make graph square
fig = matplotlib.pyplot.gcf()
fig.set_size_inches(5,5)
Another way to find the golden ratio is to use Fixed-point iteration - again, since we know that finding the fixed point of the function:
\[f(a) = \frac{a+1}{a}\]
is the golden ratio.
golden_ratio = reduce(lambda acc,_: (acc+1.0)/acc, xrange(100), 1)
print golden_ratio