Recently, I was curious if I could generate a digital radio signal from scratch just using math, and use that signal to control this radio-controlled outlet that I have.

Here's the Github source: https://github.com/calebmadrigal/radio-hacking-scripts/blob/master/radio_signal_generation.ipynb

Generating radio signals

I want to be able to generate modulated digital signals such as this one...

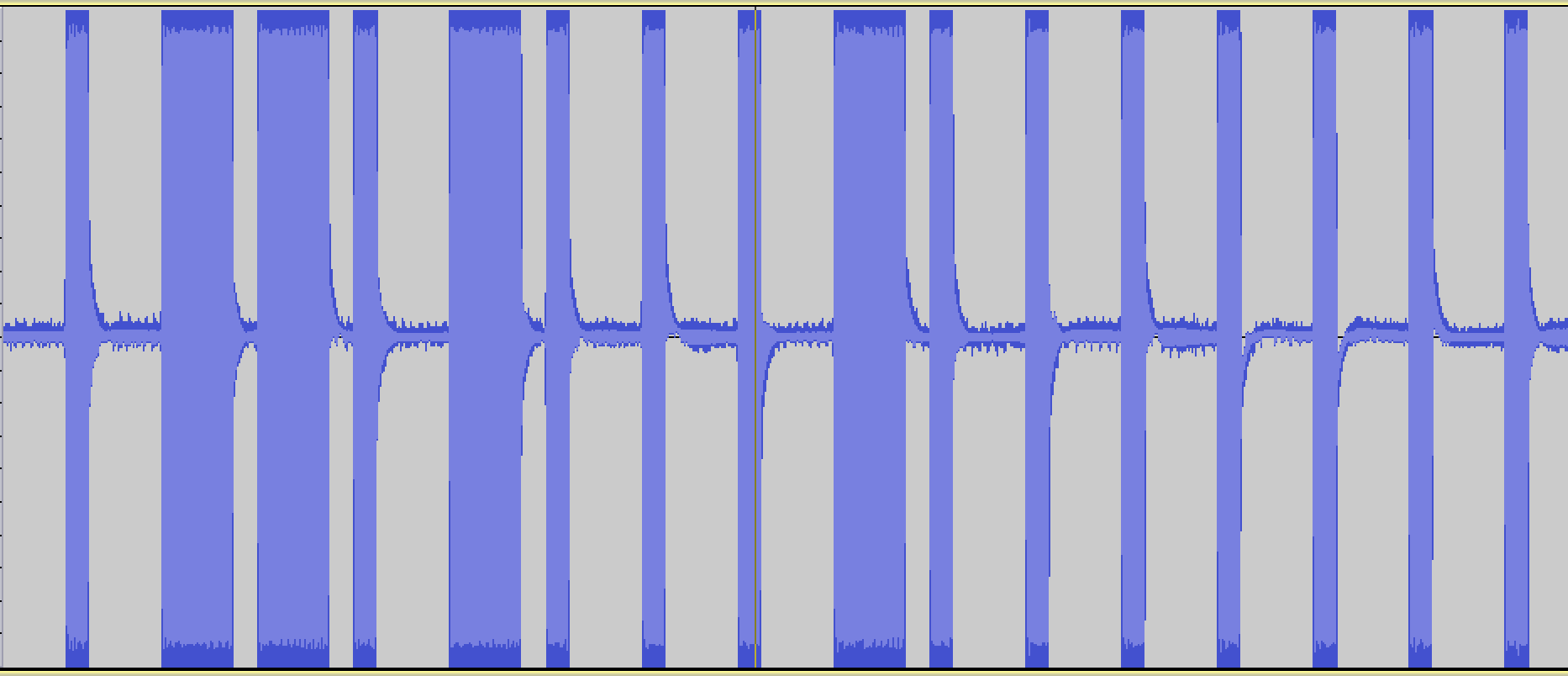
original radio signal

This is a binary signal coded with On-off keying (also known as Amplitude-shift keying).

I'm taking the long pulses to mean "1" and the short pulses to mean "0", so this signal is transmitting the digital code, "0110100010000000".

# Imports and boilerplate to make graphs look better
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import scipy
import wave
from ...

The following are my notes from a talk I gave at OSCON 2013. Here is the Github source of these Jupyter/IPython notebooks: https://github.com/calebmadrigal/FourierTalkOSCON

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import ...

I recently was car shopping, and I had the question about gas mileage: "How much does, say, the difference between 25 mpg and 30 mpg cost?"

To answer this question, I did a bit of analysis using IPython Notebook...

price_per_gallon = 4 ...

IPython Notebook provides hook methods like _repr_html_ which can be defined by Python objects to allow richer representations. Here's an example:

class ListTable(list):
    """ Overridden list class which takes a 2-dimensional list of 
        the form [[1,2,3],[4,5,6]], and renders an HTML Table in 
        IPython Notebook. """
    
    def _repr_html_(self):
        html = ["<table>"]
        for row in self:
            html.append("<tr>")
            
            for col in row:
                html.append("<td>{0}</td>".format(col))
            
            html.append("</tr>")
        html.append("</table>")
        return ''.join(html)

import random
table = ListTable()
table.append(['x', 'y', 'x-y', '(x-y)^2'])
for i in xrange(7):
    x = random.uniform(0, 10)
    y = random.uniform(0, 10)
    table.append([x, y, x-y, (x-y)**2])
table

Simple example to show how to draw lines with Matplotlib (in IPython Notebook).

ipython notebook --pylab inline

In [5]:

import matplotlib.lines as lines
fig, ax = plt.subplots()

fig.set_size_inches(6,6)          # Make graph square
scatter([-0.1],[-0.1],s=0.01)     # Move graph window a little left and down

line1 = [(0,0), (1,0)]
line2 = [(0,0), (0,1)]

# Note that the Line2D takes a list of x values and a list of y values,
# not 2 points as one might expect.  So we have to convert our points
# an x-list and a y-list.
(line1_xs, line1_ys) = zip(*line1)
(line2_xs, line2_ys) = zip(*line2)

ax.add_line(Line2D(line1_xs, line1_ys, linewidth=2, color='blue'))
ax.add_line(Line2D(line2_xs, line2_ys, linewidth=2, color='red'))
plot()
show()

Read On ↵

Is there a way to do the opposite of what the zip() function does? It turns out, there is - the zip() function with list unpacking...

x = [1,2,3,4,5]
y = [10,20,30,40,50]
points = zip(x,y)
points

[(1, 10), (2, 20), (3, 30), (4, 40), (5, 50)]

zip(*points)

[(1, 2, 3, 4, 5), (10, 20, 30, 40, 50)]

import random
rand = lambda: random.gauss(mu=1, sigma=1)
points = [(rand(), rand()) for i in xrange(1000)]

# Make the graph square
fig = plt ...

I recently migrated my blog from Wordpress to Pelican. Pelican is a static-site generating blog system which is written in Python and uses Jinja2 for templating. I'll probably do a post about the migration process later, but for now, I'll just give my reasons for moving to Pelican...

Data Longevity

I didn't want my blog data stored in a database; I vastly prefer it being stored in version-controlled Markdown format.

Markdown

• I wanted to write blog posts in Markdown (which is possible in Wordpress, but Wordpress isn't designed to use Markdown).
• I also get to use vim to write my blog posts now, which is much nicer than the Wordpress editor.

Language

• I hate PHP, but love Python. It worried me that my blog ...

Overview

This is a guide to set up IPython Notebook on a Server - specifically, on a DigitalOcean VPS. This will allow you to access your iPython Notebooks from anywhere.

Overview of Steps:

• Set up a domain name
• Get a VPS
• Install IPython Notebook (and all dependencies)
• Configure IPython Notebook to run in a server mode
• Add SSL
• Make IPython Notebook start automatically

Create a domain

Go to http://freedns.afraid.org and click "Setup an account here" Go through the signup form Click on the activation link they send to your email This will bring you back to their site; Click the link you see there called "Add a subdomain" Here is how I filled out the form:

Notes:

• Leave the Destination alone for now, and leave the ...

I've been doing a good bit of graphing in IPython Notebook recently, and I often wanted to make the graphs larger. I also often wanted to label the graph axes. So I wrote this simple function and have been using it a lot.

# Graphing helper function
def setup_graph(title='', x_label='', y_label='', fig_size=None):
    fig = plt.figure()
    if fig_size != None:
        fig.set_size_inches(fig_size[0], fig_size[1])
    ax = fig.add_subplot(111)
    ax.set_title(title)
    ax.set_xlabel(x_label)
    ax.set_ylabel(y_label)

Here's a demo of using it...

x = linspace(0, 2 * pi, 1000)
y = 5 * sin(1 * 2*pi*x) + 4 * sin(2 * 2*pi*x)

In [24]:

_ = plot(x, y)

Read On ↵

I've recently been playing with the pandas Python data analysis framework while reading the Python for Data Analysis book (which is written by the author of the pandas library). Here are 2 of my IPython Notebooks that demonstrate some of the basics:

• IPython Notebook Viewer
• US Names Examples
  • This is an example from the book which I've made some modifications to.

And here's a little screenshot of what it looks like in IPython Notebook:

I recently was exploring the Golden Ratio. I was really surprised what a simple (and recursive) relationship it comes from:

Starting with this this image, here is the derivation of the golden ratio...

IPython Notebook / Matplotlib / Pylab / Numpy is great for graphing (among other things). Below is a simple demo of how to graph with it.

To run IPython Notebook, use this command: ipython notebook --pylab inline

Here's a screenshot:

Here's an embedded IPython Notebook showing a slightly easier way:

In [5]:

x = linspace(0, 2*pi, 42)
f1 = 5 * sin(x)
f2 = 2 * sin(2*x)
f3 = 1 * sin(3*x)
plot(x, f1)
plot(x, f2, 'ro')
plot(x, f3, 'g--')
show()

Read On ↵