I'm taking the Stanford Machine Learning class. The first algorithm we covered is Linear Regression using Gradient Descent. I implemented this algorithm is Python. Here's what it looks like:
import subprocess
def create_hypothesis(slope, y0):
return lambda x: slope*x + y0
def linear_regression(data_points, learning_rate=0.01, variance=0.001):
""" Takes a set of data points in the form: [(1,1), (2,2), ...] and outputs (slope, y0). """
slope_guess = 1.
y0_guess = 1.
last_slope = 1000.
last_y0 = 1000.
num_points = len(data_points)
while (abs(slope_guess-last_slope) > variance or abs(y0_guess - last_y0) > variance):
last_slope = slope_guess
last_y0 = y0_guess
hypothesis = create_hypothesis(slope_guess, y0_guess)
y0_guess = y0_guess - learning_rate * (1./num_points) * sum([hypothesis(point[0]) - point[1] for point in data_points])
slope_guess = slope_guess - learning_rate * (1./num_points) * sum([ (hypothesis(point[0]) - point[1]) * point[0] for point in data_points])
return (slope_guess, y0_guess)
def plot_data_and_line(line, data_file):
# Plot with gnuplot
plot = subprocess.Popen(['gnuplot'], stdin=subprocess.PIPE)
line_eq = "%f*x+%f" % line
plot.communicate("plot %s, '%s' with points;" % (line_eq,data_file))
if __name__ == "__main__":
data_file = "points.dat"
points_str = [line.strip().split('\t') for line in open(data_file,'r').readlines()]
points = [(float(x),float(y)) for (x,y) in points_str]
line = linear_regression(points)
print line
plot_data_and_line(line, data_file)
This code takes in a data file with a data point on each line with the x and y separated by a TAB; Example:
0.000000 95.364693
1.000000 97.217205
2.000000 75.195834
3.000000 60.105519
This code also plots the data points and the resulting best-fit line in gnuplot. For example:
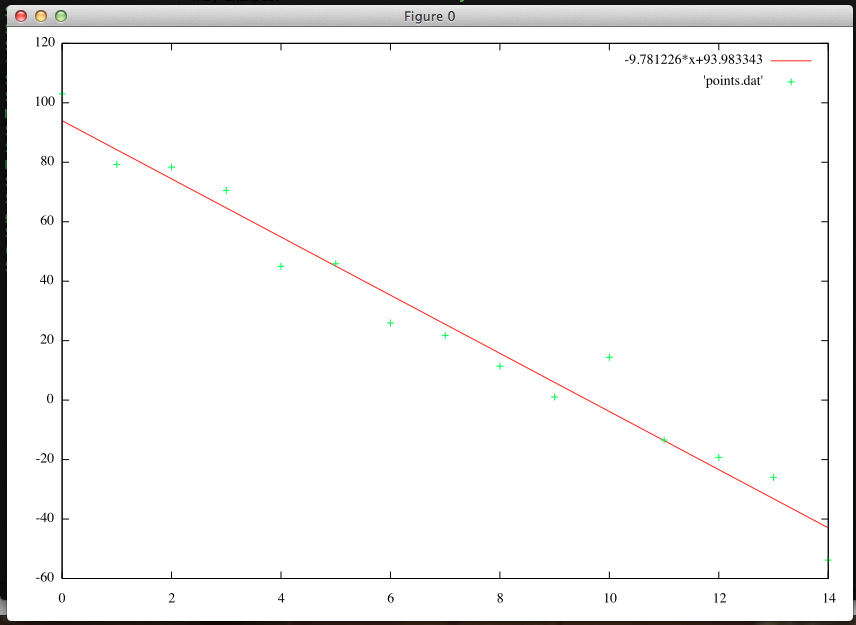
This code, along with helper files, is on my github repo.